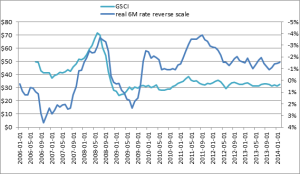
Natural gas prices are more volatile during the winter heating season. I’ve adapted the code from Data Analysis for the Life Sciences to use natural gas daily price change and simulate a p-value.
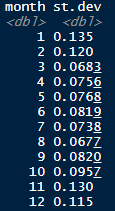
Actual monthly natural gas volatility since 2010:
ng1 %>% group_by(month) %>% summarize(st.dev = sd(ng.diff)) #find the st. dev. of each month’s prices
Separate daily natural gas prices into winter and not winter:
ng.not.winter <- ng1 %>% dplyr::filter(!month %in% c(“1”, “2”)) #control group
ng.winter <- ng1 %>% dplyr::filter(month %in% c(“1”, “2”)) #treatment group
Find the real difference in price volatility (standard deviation of price):
month.diff <- sd(ng.winter$ng1) – sd(ng.not.winter$ng1)
Create a null distribution by sampling:
set.seed(1)
n <- 10000
samp.size <- 12
null <- vector(“numeric”, n) #create a vector for the null distribution, holding the differences between means of samples from the same population
for(i in 1:n) {
ng.not.winter.sample <- sample(ng.not.winter$ng1, samp.size) #sampling from population of control
ng.winter.sample <- sample(ng.not.winter$ng1, samp.size) #sampling from population of control
null[i] <- sd(ng.winter.sample) – sd(ng.not.winter.sample)
}
mean(null >= month.diff) #p-value

Not below 5%, but not bad. The p-value would decrease if we increased the sample size.
10% of samples from the control group (non-winter) have differences greater than the true difference. This is the p-value.
hist(null, freq=TRUE)
abline(v=month.diff, col=”red”, lwd=2)

The histogram looks normal, so using a normal approximation should give a similar answer:
1 – pnorm(month.diff, mean(null), sd(null))