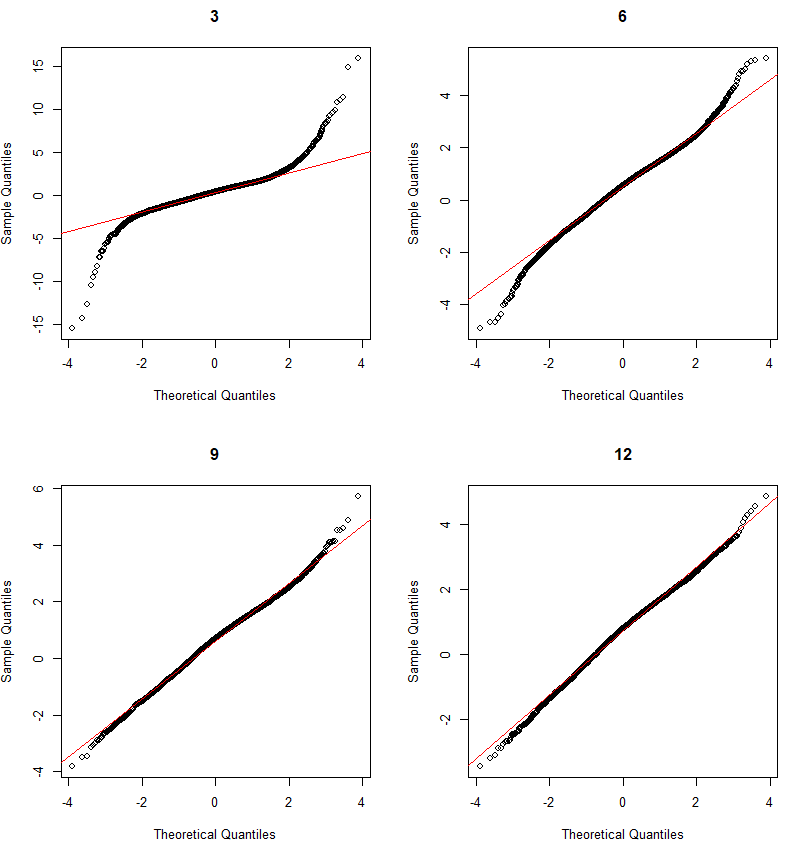
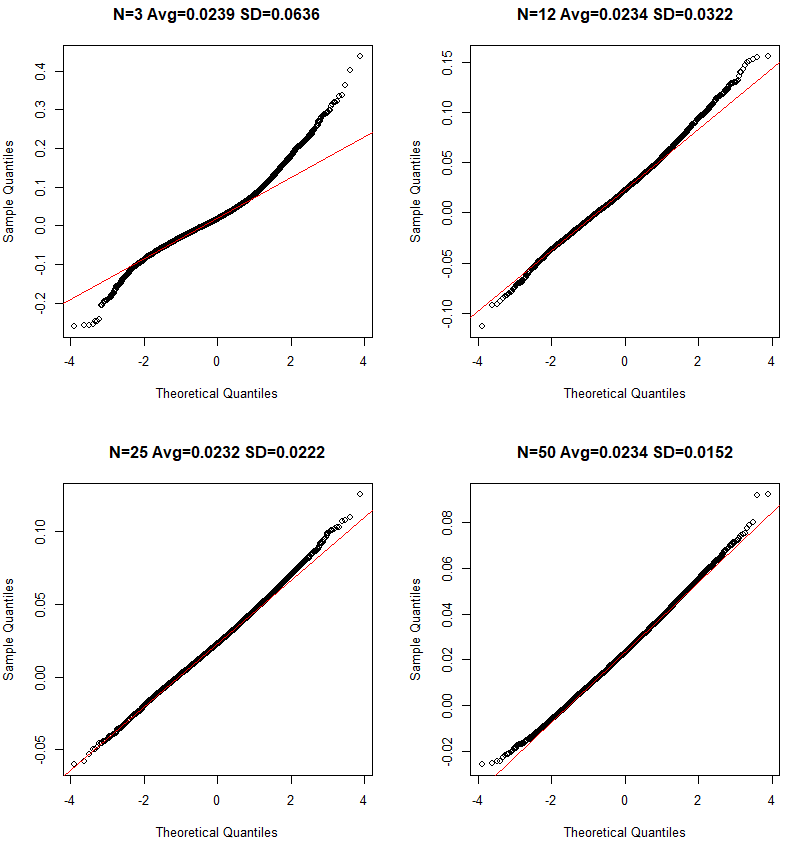
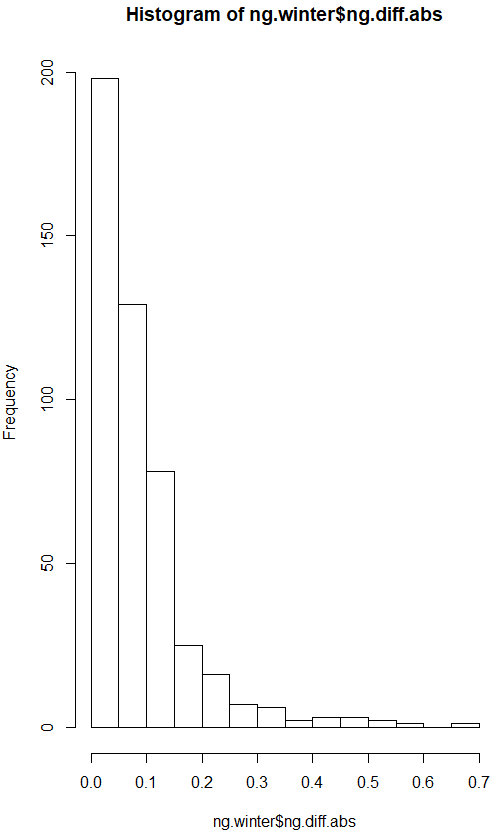
The variance of the difference of two random variables is the sum of the two variances. We sample 30 observations (usually large enough according to the CLT) from winter and not winter absolute daily price changes. The absolute daily changes appear log normal, but according to the Central Limit Theorem the distribution of the samples will be normal, assuming the sample size is large enough:

Now calculate the standard error of the difference of the sample means (or the sum of the sample means):

Calculate the difference in sample means and then calculate the t-statistic. Dividing a random variable (diff) by its own standard error gives a new random variable with a standard error of 1:

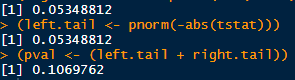
Tstat should be approximately normal with mean 0 and se 1. Assuming that tstat is normal, how often would a normally distributed random variable exceed tstat? The p-value is .107, not statistically significant at the common .05 level: